Zitat:
Zitat von TomS
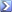
Wenn du in einem Punkt P der Mannigfaltigkeit M eine Tangentialebene definierst, dann entspricht diese lokal in P einen Tangentialvektorraum TM(P) - und in diesem Raum „leben“ deine Koordinatensysteme.
https://de.m.wikipedia.org/wiki/Tangentialraum |
Ich bin noch gerade dabei, das hier zu verstehen:
Zitat:
|
Ein einfaches Beispiel ist der Übergang von kartesischen Koordinaten in der Ebene zu Polarkoordinaten. Jeder Ortsvektor des zweidimensionalen euklidischen Raumes lässt sich bei dieser Darstellung durch die Koordinaten r ∈ [ 0 , ∞ [ ...
|
https://de.m.wikipedia.org/wiki/Diff...ansformationen
Zitat:
|
Werden nun ganz allgemein alle Koordinaten des neuen Koordinatensystems bis auf eine Koordinate konstant gehalten und die einzelne Koordinate innerhalb des Definitionsbereiches verändert, entstehen im euklidischen Raum Linien, die auch als Koordinatenlinien bezeichnet werden. Im Falle der angegebenen Polarkoordinaten entstehen so bei konstanter r Koordinate konzentrische Kreise mit Radius r um den Koordinatenursprung ( x , y ) = ( 0 , 0 ) des euklidischen Koordinatensystems.
|
Also, man wandelt einen Koordinatenpunkt eines kartesischen Koordinatensystems um zu einer Polarkoordinate mit einem "Abstand zur 0" (also der Radius) und einem Winkel. Und mit dem Winkel und dem Radius baut man sich ein neues Koordinatensystem.
Der Grund, warum man es in Polarkoordinaten umwandelt liegt wohl darin, dass man erst diese ableiten kann.
Okay, das heisst es geht dann hier weiter:
https://de.m.wikipedia.org/wiki/Part...ung#Beispiel_1
Man nimmt eine Variable als konstant an. Da bei einer Ableitung Konstanten wegfallen, kann man so eine andere Variable ableiten.
Heisst das dann, dass ich bei unendlich vielen Variablen alle bis auf eine als Konstant annehmen muss, wenn ich diese Ableiten will und damit "unendlich-1" Lösungen besitze?
Yep:
Zitat:
|
Bis auf eine Variable werden alle anderen Variablen als konstant angenommen, bezüglich dieser einen Variablen wird der Differenzialquotient bestimmt. Als Ergebnis erhält man die partielle Ableitung der Funktion nach dieser einen Variablen.
|
Man muss nur einen Absatz weiter lesen^^