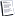 Einstein Hilbert Wirkung
Einstein Hilbert Wirkung
Vielleicht sollte ich nochmal bei Null anfangen.
Es gibt schließlich eine exakte Lösung für ein Vierervolumen-Integral über die Einstein-Gleichung.
Die Einstein-Hilbert-Wirkung, die zusammen mit der Lagrangedichte eines Materie-Feldes als zweite Lagrange-Dichte für eine kanonische oder kovariante Quantisierung angesetzt wird.
Aber diese exakte Lösung enthält schon implizit die Planck-Fläche, auch wenn man es erst nach einer kleinen Umformung sieht:
S = c^3/(16pi*y) * INT (Wurzel(det(guv)) * R (guv) *d^4x
S ist die Wirkung.
Dann ist S*16pi*y/c^3 automatisch eine Fläche..
Das klassische Feld ergibt sich aus dem Prinzip der kleinsten Wirkung, nach dem Variationsprinzip.
dS = 0
Ruv - 1/2 guv R = 0
Das bedeutet zunächst nichts anderes, als dass das dynamische Feld eine (vierdimensionale) Form annimmt, dessen Wirkungsintegral extremal wird, im allgemeinen minimal. Das Integral ist positiv definit. Das Minimum kann minimal Null sein. Aber letztlich ist das nicht relevant. Relevant ist nur, dass dieses Integral nur ein Extremum aufweist - zumindest klassisch gerechnet!
Wenn ich nun aber direkt bei der EH-Wirkung ansetze - und explizit das Wirkungsquant als nicht unterschreitbare Größe in die Formel einbringe - kann das Integral nicht jeden beliebigen Wert annehmen und besonders nicht Null werden:
S = N * h = c^3/(16pi*y) * INT (Wurzel(det(guv)) * R (guv) *d^4x
Das bedeutet für die Fläche:
N*h*16pi*y/c^3 = N* 32pi^2 * Apl (Planckfläche)
Das Variationsprinzip bedeutet dann zunächst, dass das Vierervolumenintegral zu einer Mindestfläche führt. Genauer ausgedrückt: Es führt zu einer nicht unterschreitbaren Flächenänderung. Einer skalaren Flächenänderung.
Aber dies bedingt auch, dass die kleinstmögliche Fläche denselben Betrag aufweist.
Um den Ansatz zu verallgemeinern habe ich nur folgende Überlegung dazu:
Eine Fläche ist eine orientierte Größe. Sie hat Betrag und Richtung!
Will ich sie aber koordinatenfrei ausdrücken, muss ich sie als Tensor zweiter Stufe schreiben.
Also, kann ich die skalare Wirkung, als Skalar eines Tensors zweiter Stufe interpretieren?
Indirekt: ja.
Es handelt sich ja nur um eine Konstante. Der eigentliche Parameter ist N, als Betrag des Richtungsvektors V der Fläche.
Ansatz:
N*32pi^2*Apl* V(uv) * g(hoch:uv) = g(hoch:uv) * INT (Wurzel(det(guv)) * R (guv) *d^4x
Jetzt noch meine Aufhebung des Integrals auf der rechten Seite als kovariante Ableitung auf der linken Seite der Gleichung:
A(uv,w) * g(hoch:uv) = g(hoch:uv) * INT (Wurzel(det(guv)) * R (guv) *d^3x
A(uv,w,y) * g(hoch:uv) = g(hoch:uv) * INT (Wurzel(det(guv)) * R (guv) *d^2x
Fehlt nur noch die durchströmte Fläche, durch die der durch die erste Ableitung definierte Impuls P(uvw) fließt. Ab hier wird das Problem zunächst vieldeutig.
Als nächstes will ich nochmal die "normale" kanonische Quantisierung zum Vergleich bringen.
MfG ghosti
__________________
Koordinatensysteme sind die Extremstform von Egoisten- sie beziehen alles auf sich selbst.
http://thorsworld.net/
|