Zitat:
Zitat von zeitgenosse
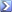
dP/dt = α P
...
Nun aber beginnt erst die eigentliche Aufgabe des Naturwissenschaftlers, indem diese DGL auch gelöst werden muss. Es gilt somit, alle diejenigen Funktionen zu finden, die dieser DGL genügen. Nach reiflicher Überlegung (man konsultiere ggf. den Bronstein) gelangt man schliesslich zur allgemeinen
|
Das geht hier noch ganz elementar mit dem Standard-Verfahren "Separation der Variablen", d.h. alle P's auf die eine Seite und die t's auf die andere bringen. Wo das geht, hat man gute Chancen, eine Lösung zu finden. Ist hier trivial:
dP/P = a dt
und nun kann man direkt integrieren (Stammfunktion von 1/P ist ja der natürliche Logarithmus)
ln P - ln Po = a (t - to)
Nach Exponentiation
P/Po = exp [a (t - to)]
P = Po exp [a (t - to)]
Dabei steht ln für den natürlichen Logarithmus und Po für P zur Zeit to - die sog. Anfangsbedingung.
Zitat:
|
Zitat von zeitgenosse
Lösung:
P(t) = C * e^αt ; mit einer beliebigen reellen Konstanten C
Besitzt die Population zum Zeitpunkt t_o = 0 die Grösse P_o folgt daraus:
P(t) = P_o * e^αt
Die Anfangsgrösse P_o und das lokale Wachstumsgesetz legen somit eindeutig die Grösse in jedem Zeitpunkt t ≥ 0 fest. Damit haben wir das Wachstumsgesetz im Grossen gefunden. Aus naheliegenden Gründen nennt man es ein "exponentielles Wachstumsgesetz".
Gr. zg
|