"Crashkurs" Topologie

[JoAx]

Hallo SCR!

Ich bin auch dabei, die Topologie einzuordnen, was mir bis jetzt aber, nach eigenem Einschätzen, nicht wirklich gelingt. Also -> alles imho:

Zitat von SCR

Das ist im Groben MEIN Bild "der Topologie". Ob es 100%ig richtig ist weiß ich nicht

Was mir da auffällt, ist - dass du imho Geometrie und Topologie zu sehr vermischst (zu wenig von einander abgrenzt). Bspl.:

Topologie:

- Offene Kugel mit Radius R: alle Punkte mit dem Abstand r<R
- Abgeschlossene offene Kugel mit Radius R: alle Punkte mit dem Abstand r=<R

Zitat von wiki

Die Topologie untersucht die Eigenschaften geometrischer Körper

Geometrischer Körper = Teilmenge.

Ich komme gleich auf den Punkt - Topologische Räume haben immer einen Rand. Dieser mag zwar zur Menge nicht zu gehören ("offene Menge"), es gibt diesen aber dennoch. Über die geometrische "Beschaffenheit" des (ganzen) Randes kann man die Topologie des Körpers selbst bestimmen.

Wie sind aber die Beziehungen zwischen einzelnen Elementen/Punkten der (Teil-) Menge?
Abstand, Winkel?
Die sind euklidisch, wenn die Menge (nicht Teilmenge) euklidisch ist.


Gruß, Johann

[eigenvector]

Zitat von JoAx

Ich komme gleich auf den Punkt - Topologische Räume haben immer einen Rand. Dieser mag zwar zur Menge nicht zu gehören ("offene Menge"), es gibt diesen aber dennoch. Über die geometrische "Beschaffenheit" des (ganzen) Randes kann man die Topologie des Körpers selbst bestimmen.

Das hört sich ein bisschen komisch an.
Eine leere Menge ist per Definition offen, somit ist ein Topologischer Raum als Menge in sich immer abgeschlossen (und außerdem per Definition offen). Der Rand ist also immer dabei.

[JoAx]

Hallo eigenvektor!

Zitat von eigenvector

Das hört sich ein bisschen komisch an.
Eine leere Menge ist per Definition offen, somit ist ein Topologischer Raum als Menge in sich immer abgeschlossen (und außerdem per Definition offen). Der Rand ist also immer dabei.

Warum soll daraus, dass eine leere Menge per Definition offen ist, folgen, dass ein (beliebiger) topologischer Raum immer (in sich?) abgeschlossen und offen sein soll?

offener Raum: -1<x<1 - der Rand gehört nicht zur Menge
abgeschlossener Raum: -1≤x≤1 - der Rand gehört zur Menge

?

Gruß, Johann

NACHTRAG:
Da fällt mir noch etwas zu "Batzen"/"kein Batzen" ein.

A: -10<a<10
B: -5≤b≤5
C = A - B: -10<c<-5 ∪ 5<c<10

[SCR]

Hallo JoAx, Hallo eigenvector,

Zitat von JoAx

Was mir da auffällt, ist - dass du imho Geometrie und Topologie zu sehr vermischst (zu wenig von einander abgrenzt).

Ja (?):

Zitat von wikipedia

Die Topologie (gr. τόπος, tópos, „Ort“, „Platz“ und -logie) oder Analysis situs, wie sie früher meistens genannt wurde, ist ein Teilgebiet der Mathematik. Sie ist im Wesentlichen eine Schöpfung des 20. Jahrhunderts und bereits seit Jahrzehnten als Grundlagenfach anerkannt. Insofern hat sie (zusammen unter anderem mit der linearen Algebra und der Maßtheorie) das Erbe der Geometrie angetreten.

http://de.wikipedia.org/wiki/Geometrische_Topologie

Wie stellen sich die Universitäten bezüglich der Topologie auf? (Das sind jetzt einfach einmal die ersten drei Google-Treffer):
http://www.mathematik.uni-muenchen.d...top/index.html
http://www.mathematik.uni-osnabrueck...r=ag-topologie
http://www.math.uni-bielefeld.de/~geotop/
...

Zum Thema "offen" bzw. "geschlossen":

Man betrachte hierzu mein Avatar: Ein Kubus ist homöomorph zu einer Sphäre -> Eine Kugel kann man so "kneten", dass ihre positiven Krümmungen ausschließlich in den Kanten zum Tragen kommen - Der Rest des Körpers (= alle Seitenflächen) ist flach:



Gleiches gilt für einen (kompletten) Zylinder (= "mit Deckel"):



Auch hier wurden die positiven Krümmungen "in der Kante konzentriert":



Das Vorhandensein von "Kanten", die nicht nur reine äußere Krümmungen (wie diese z.B. beim Zerknüllen eines Blattes Papier entstehen) darstellen, sondern gleichzeitig innere Krümmungen repräsentieren, erfordern es, dass der topologisch betrachtete Körper abgeschlossen ist -> Ein offener Kubus bzw. Zylinder (ohne Löcher) ist (meines Wissens auch laut Lehrbuch) flach.

Zitat von JoAx

C = A - B: -10<c<-5 ∪ 5<c<10

bzw. 5i < ci < 10i (?)

[JoAx]

Zitat von SCR

Ja (?):

Ich denke schon SCR, auch wenn ich mich irren kann.
Ich sehe das laienhaft so, dass man die Topologie nicht ohne Geometrie betreiben kann. Umgekehrt geht das aber.

Alle Körper, die du vorführst haben einen Rand. Für eine Kugel wäre das r=R. Die Flache, die den Rand "bildet", hat aber selbst keinen Rand.


Gruß, Johann

[SCR]

Hallo JoAx,

Zitat von JoAx

Alle Körper, die du vorführst haben einen Rand. Für eine Kugel wäre das r=R. Die Flache, die den Rand "bildet", hat aber selbst keinen Rand.

Ja, der "Rand" ist IMHO entscheidend ... vielleicht sollten wir das Thema einmal an Hand eines konkreten Praxis-Beispiels diskutieren:

Das flamm'sche Paraboloid (= Äußere Schwarzschildlösung) lässt sich in drei Bereiche aufteilen (von außen nach innen):
1. Bereich: "Die Schwarzschildmetrik geht asymptotisch im Unendlichen in die Minkowski-Metrik über"
-> Wir betrachten einen offenen, "unendlichen" Körper -> Hier fehlen IMHO schlichtweg die "äußeren", positiven Krümmungen eines "typischen Batzens".
2. Bereich: Das "Oberteil" eines Hyperboloiden -> Negative Krümmungen.
3. Bereich: Die Koordinaten-Singularität / Der EH führen topologisch betrachtet zu einem Loch.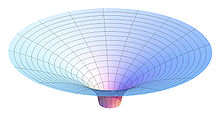


(Quelle: wikipedia; Bereich 1 nicht abgebildet)

-> Vom topologischen Standpunkt aus betrachtet müsste das Flamm'sche Paraboloid nergativ gekrümmt sein.

Innere Schwarzschildlösung:
Die innere Schwarzschildlösung beschreibt eine Sphäre

-> Vom topologischen Standpunkt aus betrachtet müsste die innere Schwarzschildlösung positiv gekrümmt sein.

Die vollständige Schwarzschildlösung ergibt sich aus der Kombination der äußeren mit der inneren Schwarzschildlösung:

(Quelle: wikipedia)

"Das Loch" wurde geschlossen = Die negativen Krümmungen der äußeren Lösung heben sich mit den positiven Krümmungen der inneren Lösung auf

-> Vom topologischen Standpunkt aus betrachtet müsste sich die vollständige Schwarzschildlösung global gesehen flach darstellen.

Wie seht Ihr das?

Anmerkung: Die "äußere flache Minkowski-Metrik" findet man nur im Modell und nicht in der Realität.

[JoAx]

Hallo SCR!

Zitat von SCR

(Quelle: wikipedia; Bereich 1 nicht abgebildet)

-> Vom topologischen Standpunkt aus betrachtet müsste das Flamm'sche Paraboloid nergativ gekrümmt sein.

Kannst du mir bitte erklären, wo/wann es bei der Topologie (nicht Geometrie) überhaupt um Krümmungen geht?

Bei der ART geht es doch ausschließlich um Geometrie, oder nicht? Das ganze Universum oder auch nur begrenzte bereiche davon werden geometrisch, und nicht topologisch behandelt. (?)

Zitat von SCR

Innere Schwarzschildlösung:
Die innere Schwarzschildlösung beschreibt eine Sphäre

-> Vom topologischen Standpunkt aus betrachtet müsste die innere Schwarzschildlösung positiv gekrümmt sein.

Auch hier - ...

Zitat von SCR

Wie seht Ihr das?

Meine Einschätzung sollte klar geworden sein. Oder?

Zitat von SCR

Anmerkung: Die "äußere flache Minkowski-Metrik" findet man nur im Modell und nicht in der Realität.

Das ist völlig überflüssig. Die Minkowski-Metrik im Unendlichen ist eine Randbedingung. Unter anderem auch diese macht es überhaupt möglich irgendeine Lösung zu finden.


Gruß, Johann

[SCR]

Hallo JoAx,

Zitat von JoAx

Kannst du mir bitte erklären, wo/wann es bei der Topologie (nicht Geometrie) überhaupt um Krümmungen geht?

Die äußere Gestalt eines Körpers/Raums (= Topologie) erlaubt Dir globale Aussagen über die inneren Krümmungen (= Geometrie) des Körpers/Raums.
Exemplarisch aus

Zitat von SCR

Um einen ersten groben Überblick zu gewinnen, mit was sich die Topologie beschäftigt (und auf welcher Basis), kann ich diesen IMHO hervorragenden Artikel nur wärmstens empfehlen: Die Lösung eines Jahrhundertproblems; Spektrum der Wissenschaft; 11/2004

Zitat von JoAx

Bei der ART geht es doch ausschließlich um Geometrie, oder nicht? Das ganze Universum oder auch nur begrenzte bereiche davon werden geometrisch, und nicht topologisch behandelt. (?)

Was hast Du denn eigentlich gegen die Topologie / Warum willst Du sie unbedingt von der Geometrie abgrenzen? Verstehe ich nicht ganz.

Zitat von JoAx

Das ist völlig überflüssig. Die Minkowski-Metrik im Unendlichen ist eine Randbedingung. Unter anderem auch diese macht es überhaupt möglich irgendeine Lösung zu finden.

Zitat von Pathfinder

Und mit diesem "topologischen Grundwissen" schaue ich mir jetzt einmal die Schwarzschildlösung "von außen" an. Da erkenne ich sofort zwei "Krümmungsprobleme": Eines im Zentrum, eines außenherum.

Die äußere Lösung weist "im Zentrum" durch die Singularität ein Loch in der Mannigfaltigkeit auf -> Ein Loch von außen betrachtet bedeutet stets, dass negative äußere wie auch innere Krümmungen vorliegen (k<0).

Alle Schwarzschildlösungen weisen außen das Problem ihrer Offenheit auf: "Die Schwarzschildmetrik geht asymptotisch nach außen hin in die Minowskimetrik über". Das entspricht ja nun keinesfalls der Realität: In einem Universum bestehend aus nur einer Zentralmasse werden wir keinen Ort finden, an welchem nicht die Gravitation derselben Auswirkung zeigen würde -> Die Schwarzschildlösung eignet sich deshalb auch nicht als kosmologisches Modell sondern nur als lokal anwendbare Lösung.

Nun kann ich das "innere Krümmungsproblem" (es handelt sich lediglich um eine Koordinatensingularität) dadurch beheben, dass ich die äußere um die innere zur vollständigen Schwarzschildlösung ergänze.
Topologisch betrachtet "verschwindet dadurch das Loch" und damit auch die äußeren wie auch die inneren (diese in Summe: negative und positive innere Krümmungen heben sich gegenseitig auf) Krümmungen der Mannigfaltigkeit -> k=0 bei Zugrundelegung der vollständigen Schwarzschildlösung.

Um das "äußere Krümmungsproblem" zu beheben bringe ich die Mannigfaltigkeit "mit sich selbst zum Abschluß" -> Ich "nehme die Schere" und ergänze außen positive Krümmungen (Siehe den gebastelten Globus von oben) bis eine geschlossene Mannigfaltigkeit vorliegt (~ "Jetzt wirkt die Gravitation überall" weil jetzt überall innere Krümmungen vorliegen).

Ergebnis:
Diese "modifizierte" vollständige Schwarzschildlösung würde nun auch die "eigentlich korrekte" Schnittkrümmung aufweisen: k>0.
Denn jetzt haben wir nur noch einen Batzen Knet vor uns liegen - Und der ist positiv gekrümmt. Von außen als auch von innen betrachtet.

So ungefähr verstehe ich "topologische Physik".

[eigenvector]

Zitat von JoAx

Warum soll daraus, dass eine leere Menge per Definition offen ist, folgen, dass ein (beliebiger) topologischer Raum immer (in sich?) abgeschlossen und offen sein soll?

Dass der gesamte Topologische Raum offen ist, gilt per Definition.
Das Komplement der Leeren Menge ist der gesamte Topologische Raum. Das Komplement einer offenen Menge ist abgeschlossen. Also ist der gesamte Topologische Raum abgeschlossen.

[JoAx]

Hallo eigenvector!

Zitat von eigenvector

Dass der gesamte Topologische Raum offen ist, gilt per Definition.
Das Komplement der Leeren Menge ist der gesamte Topologische Raum. Das Komplement einer offenen Menge ist abgeschlossen. Also ist der gesamte Topologische Raum abgeschlossen.

Wo liegt mein Fehler?
In der Verwendung von 'Menge', wo 'Teilmenge' verwendet werden musste?
Oder ... ?


Gruß, Johann