Math Schwingungs DZGL

[richy]

Zitat von Marco

Er kann ja Graf Maple aus der Wurstfachabteilung fragen.

Zum Beispiel :-)
Aber um z.B. diese Konvergenzzentrum-Radiustransformation weiter zu untersuchen wird Graf Maple alleine nicht ausreichen. Da muss man schon das Maple Orakel selbst befragen. Ich kann mir auch schon vorstellen wie es antworten wird. Mit gar garstig Kettenwurzel
In der eleganten Version mit nicht weniger ueblen Polynomen.
Es sieht ja so aus, dass im Grunde alle Fragen bezueglich der Merman DZGL geklaert sind. Wiki hat zu recht Mermans graphisch motivierte Naeherung abgelehnt. Denn warum sollte ich etwas annaehern wenn es ueber die Addditionstheoreme auch exakt geht ? :-)
c1=cos(dt)
c2=sin(dt)
Wie bereits erwaehnt habe ich das daraus resultierende DZGL System schon vor 20 Jahren mal hergeleitet (dann wieder vergessen) und mich damals genauso wie Merman wohl jetzt gewundet warum das denn ueberhaupt funktioniert. Na wegen den Additionstheoremen. So koennte man dies abhaken. Aber mir scheint, dass es vielleicht zu voreilig waere dieses diskrete Simulationsprinzip damit abzuhaken. So wie seitens Wiki.
Das besondere daran ist z.B. dass es eben nicht auf dem klassischen Strickmuster der numerischen Simulation basiert. Das da lautet :
Ersetze die Differential und Integraloperatoren durch Differenzenausdruecke.
Nee, so funktioniert das nicht. Man erkennt dies alleine daran, dass x(k),y(k) mit einem Vorfaktor behaftet sind. Und dass die Simulation eben voellig exakt ist. Ich meine eine durchaus interessante Sache, die es sich lohnt noch etwas weiter zu untersuchen. Und ich bin Merman fuer diesen erneuten Gedankenanstoss durchaus dankbar.
Gruesse

[richy]

Ob ein dreijaehriges Kind das Programmpaket MAPLE als ein geeignetes Weihnachtsgeschenk akzeptieren wuerde steht natuerlich auf einem ganz anderen Blatt.

[mermanview]

Hallo richy:

du verwirrst,

ich glaube du hast die Methode "Additionstheorem" sowohl für die Bestimmung der Folgewerte, als auch zur Herleitung der Konstanten c1, c2 beschrieben.

Und alle weiteren Betrachtungen koennten wir uns im Grunde sparen, denn wir wissen aus den Additionstheoremen wie wir C1 und C2 waehlen muessen, dass die Iteration unsere Sinus Koninussimulation sogar voellig exakt ist. (Ja, das ist etwas eigentuemlich)

C1=cos(2*Pi/N)
C2=sin(2*Pi/N)

An anderer Stelle verwendest du den Begriff "Taylorreihe" als Methode um die Konstanten c1 und c2 zu ermitteln.

Es ist klar, dass Abtastwerte N und "Körnungswert" n nicht 360 und 2Pi/360 sein müssen. ebenso ist klar, dass bei genauer Bestimmung der Konstanten c1, c2 die Folgewerte genau sind.

Dass damit der größte Teil der Aufgabe gelöst ist, ja sogar für die Softwareanwendung evtl. Vorteile bestehen ist auch klar.

Es bleibt mir vorbehalten die Genauigkeit meiner Näherungsmethode in eigenem C -Programm zu testen, in dem ich m0 verkleinere (und Wurzelziehen vermeide).

Ich hätte nichts gegen einen MAPLE-Download, ich weiß nur nicht ob ich mich in gewünschter Schnelligkeit einarbeiten würde.
Ich habe noch zweieinhalb unfertige humanoide Roboter in meiner Werkstatt stehen, die werden seit ca. zwei Jahren um ein 100stel pro drei Monaten weitergearbeitet, die hätten eigentlich Vorrang vor MAPLE.

Job und Familie lassen, so lang die kleinen Ableger noch so klein sind, kaum Zeit, .. worüber ich mich nicht beklagen will.


Zurück zu Sinus:

Es bleibt für mich die Restaufgabe zu überprüfen, ob ich eine MATHEMATISCHE f(x) finde aus deren x Koordinaten sich y Koordinaten ergeben, so dass beide zusammen eine Sinuskurve darstellen.

Du sagst, dass das bereits vollbracht ist und nennst dafür:

Zitat:
... aber bisher ergibt die Mermansinus Formel lediglich Sinuswerte nicht aber einen Funktionsgraphen durch y=f(x).
Einspruch ! Du hast deine Aufgabenstellung, Vorgabe doch bereits zumindestens naeherungsweise geloest. Und weist wie man sie exakt loest. (Additionstheoreme). Aber nur fuer ganz bestimmte Stuetzstellen n*dt. Wir berechnen y=f(n*dt)=sin(n*2*Pi/N) N=Anzahl Abtastwerte.

Vielleicht fehlt mir die mathematische Bildung, aber das sieht für nach f(n*dt) aus, nicht nach f(x), bedenke die Doppelbenennung von x !
x steht in diesem Falle nicht wie bisher (in meiner Iteration) für den Cosinus, sondern er ist die x Achse eines Koordinatensystems, in dem die simple Sinus Kurve (aus dem Einheitskreis) abgebildet ist.

Die Wertetabelle für x strebt von 0 gegen 2Pi in sagen wir in 360 Schritten.
Die Wertetabelle für y sind die Sinuswerte, die sich aber aus den x-Werten ergeben sollen.

am Beispiel sin(30°) = 0,5:

x Koordinate = 0,523598776 = 30/360 * 2Pi
y Koordinate = 0,5

Welche Gleichung (oder Reihenberechnung) macht aus 0,523598776 -> 0,5

(Bisher können wir lediglich in 30 Schritten mit m0 und c1/c2 ->cos/sin(30°) bestimmen)

Ich vermute diese f(x) ist nicht machbar, auszuprobieren, ob ich es dennoch hinbekomme,
macht mir ebenso Spass wie dir Verhulst per DZGL Spass macht.

Muss Feierabend machen, später weiter,

Gruß Merman

PS. Raul Midon kenne ich, allerdings nur von youtube, der Mann ist der Hammer,
der Mann ist hier http://www.youtube.com/watch?v=Ddn4MGaS3N4 ist auch 'ne Klasse für sich.

[richy]

Hi merman

Ich glaube du hast die Methode "Additionstheorem" sowohl für die Bestimmung der Folgewerte, als auch zur Herleitung der Konstanten c1, c2 beschrieben.

Yepp, hier nochmals die Additionstheoreme. Und wenn man dort z.b. y=dx setzt, sieht man im Grunde sofort wie man dies fuer die Iteration ausnuetzen kann :




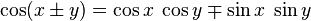Und bis auf die Konstanten cos(dx),sin(dx) entspricht die Iteration der Methode die du graphisch hergeleitet hast.

An anderer Stelle verwendest du den Begriff "Taylorreihe" als Methode um die Konstanten c1 und c2 zu ermitteln.

Weil dein C1 einer abgebrochenen Taylorreihe cos(m0)=1-m0^2/2.... entspricht. Deine graphische Methode hat zu dieser Taylorreihe fuer c1 gefuehrt. Fuer c2 fuehrte deine Methode dich auf c2=wurzel(1-c^2).
Man kann aber auch hier eine Taylorreihe verwenden : sin(m0)=m0-m0^3/6....
Und die Iteration wird damit sogar genauer.

Es bleibt mir vorbehalten die Genauigkeit meiner Näherungsmethode in eigenem C -Programm zu testen, in dem ich m0 verkleinere (und Wurzelziehen vermeide).

Ja klar. Probieren geht ueber studieren. Und probiere dann auch c2=m0-m0^3/6 aus. Wenn du m0 vekleinerst werden vor allem deine Konstanten c1 und c2 genauer, wie die Grafiken hier zeigen :

c1 :

c2:

Es bleibt für mich die Restaufgabe zu überprüfen, ob ich eine MATHEMATISCHE f(x) finde aus deren x Koordinaten sich y Koordinaten ergeben, so dass beide zusammen eine Sinuskurve darstellen.

Betrachten wir das mal etwas philosophischer. Ausgehend von ganzen Zahlen steckt in einem Kreis, in Sinus und Kosinus die Zahl Pi drin. Eine irrationale transzendente Zahl. Und damit in irgendeiner Form etwas "Unendliches". So muessten wir z.B. c1 und c2 unendlich genau bestimmen.

Du kannst deine Aufgabe auch einfach ueber die Taylorreihe loesen :
http://de.wikipedia.org/wiki/Taylorreihe


Dort gibt es auch eine nette Animation zu cos(x). Aber man benoetigt unendlich viele Terme damit die Approximation exakt waere. Wobei man mit 8 Termen im Intervall 0..2*Pi schon recht genau liegt :

cos(x)= 1 - 1/2 x^2 + 1/24 x^4 - 1/720 x^6 + 1/40320 x^8 - 1/3628800 x^10 + 1/479001600 x^12 - 1/87178291200 x^14 + 1/20922789888000 x^16

Und ueber die Methode von Gauss kann man dies noch erheblich verbessern :

(your Approximation = taylor) Jeweils nur drei Terme.
Das ist aber schon etwas mehr fuer Spezialisten.

aber das sieht für nach f(n*dt) aus, nicht nach f(x), bedenke die Doppelbenennung von x !

Die Bennenung hat nichts zu bedeuten. Die entscheidende Enschraenkung ist, dass n ganzzahlig ist und x voellig beliebig reell. Daher schrieb ich :

Aber nur fuer ganz bestimmte Stuetzstellen n*dt.

Sei dt 1 Grad dann erzeugt unsere Methode den Sinus fuer
1*1 Grad
2*1 Grad
3*1 Grad
.... e.t.c
Fuer lediglich 360 Werte. (Wobei wir noch etwas tricksen koennen)

[richy]

Welche Gleichung (oder Reihenberechnung) macht aus 0,523598776 -> 0,5

Ich wuerde dies genauer formulieren :
Welche Gleichung (oder Reihenberechnung) macht aus arcsin(0.5) -> 0,5

Der Cordic Algorithmus muss dies z.B. leisten. Denn in keinem Rechner steckt ein Kreis drin.
Ein einfacher Rechner kann hardwaremaessig nur addieren. Prozessoren fuer musikalische Anwendungen koennen dagegen auch multipilizieren.
Die Taylorapproximation ist nicht die beste Loesung, aber deine
Aufgabenstellung wuerde sie (eher "zufaellig") genau loesen :



Aber je weiter man sich von dem Entwicklungszentrum (in dem Fall x=0) entfernt, desto schlechter wir das Ergebnis. Siehe Grafiken Wiki. Da liegen wir weitaus besser !

[mermanview]

Hallo nochmal,

konnte heut Nacht zw. 2:30 und 4:30 nicht schlafen, was tun ?
-> sinus.c schreiben...

Stöhn, alleine die Vorarbeit:
- die Variabel-Deklaration für ca. 20ig-Stellige Dezimalwerte finden (long double), die dann trotzdem macht was sie will
- die richtigen Parameter ausdrucken mit "printf" printf(" %Lf "); (mit großem L, nicht wie sonst mit kleinem l)
- Zusatzoptionen "-lm" fürs Compilieren finden, damit sqrt(Variablename statt Zahl) überhaupt klappt (cc -o sinus sinus.c -lm)

Das Endergebnis entlohnte dann die Mühe mit großer Ungenauigkeit bei schlichter "Körnung", Ungenauigkeit, die mit feinerer Justierung auch noch zunahm, doppelstöhn.
(Ich vermute der Mathematiker von Wiki hat's auch mit C versucht, weswegen er irrtümlicherweise kritisierte, dass sich die Ungenauigketen akkumulieren, bei zunehmenden Iterationsschritten.

Also her mit MAPLE !

Da ich unter Linux arbeite, habe ich mal gegoogelt und folgenden Download Link gefunden (es gibt bestimmt noch mehr), hab ihn noch nicht ausprobiert:

EDIT: ich hab Link sicherheitshalber wieder rausgenommen, ich kenn mich da nicht so gut aus, er war von thepiratbay, (dezentralisierte Datenlogistik von urheberrechtlich geschützten Daten), mir persönlich gefällt die Idee zwar, aber ich will nicht mit Unbekanntem jonglieren.
(außer mit wissenschaftlichen Erkenntnissen :- D)

C -Quellcode:

#include <stdio.h>
#include <math.h>


main()
{
------long double pi, m0, x, y, c1, c2, winkel=0;
------int koernung=180, zaehler;
------pi=M_PI;
------m0=pi/koernung;
------c1=1-((m0*m0)/2);
------c2=sqrt(1-(x1*x1));
------x=x1; //Starwert für 1°
------y=y1; // Startwert für 1°
------for (zaehler=1;zaehler<koernung+1;zaehler++)
------{
-----------winkel=180/koernung*zaehler;
-----------printf("sin(%Lf °) = %.18Lf\n", winkel, y);
-----------x=(x*c1)-(y*c2);
-----------y=sqrt(1-(x*x));
------}
------return(0);
}

Habe den Quellcode hier am Arbeitsplatz ohne Testmöglichkeit noch etwas umgeschrieben, hoffe keine Fehler eingebaut zu haben.
(Mir fällt grad auf, ich hätte die Wurzelfunktion in der Schleife vermeiden können (wie besprochen), war aber auch so schon schnell)

---------------------------------------------------------------------------

Zu unserer Sinus-Funktion:

Dass alle Sinus Algos nicht um Pi herum kommen, also eine endliche Ganauigkeit haben müssen, war auch mein Gedanke, deshalb habe ich zunächst m0=Pi/180 gweählt, weil man diesen Wert später jederzeit verfeinern kann.

Ich vermute, dass ein Taschenrechner und andere Programme, sehr genäherte Startwerte verwenden (m0, c1, c2) um dann per Additionstheorem die Folgewerte zu berechnen.
Allerdings gab es da noch die Anmerkung des Wiki-Mathematikers, dass das Halbieren (und Verdoppeln?) von Winkeln die Iterationsschritte nochnal verkürze.
Ich vermute auch dahinter steckt eine die mathematische Umsetzung einer Geometrischen Logik, die in unserer Sinusfunktion noch nicht enthalten ist.
(Bildlich kann ich mir vorstellen, dass ein Dreieck mathematisch schnell halbiert ist, auf Grund gleichlanger Schenkel (ähem), insofern ließe sich jede geählte Körnung ebenso schnell halbieren, so o.ä.)

Ich bin aber froh, wenn ich meine Merman-Aproximation und die Mermanfolgewerte untersucht habe auf Ganauigkeit und Schnelligkeit, bei bloßer Verkleinerung von m0 (z.B. Pi/180, Pi/1800, Pi/18000 usw), die Winkelhalbierung ist erstmal geschenkt.

Noch zwei Punkte:

1.)
(Die Kostante c1 ist die Gleichsetzung von Strich mit Kreisbogenabschnitt, c1= 1-m0^2/2)
Meine c2 = wurzel(m0^2 - m0^4/4) ist nicht der Versuch einer Taylorreihe,
der Term entstand aus der Herleitung c2=Wurzel(1-c1^2) (mit c1 = 1- m0^2/2)

Es sind die x- und y-Koordinaten für 1° in einem Kreis.
Da dem Kreis die Kreisformel zugrunde liegt, ergibt sich für jede y-Koordinate zwingend die Herleitung: y= wurzel(1-x^2),
so auch für diese Anfangkoordinaten für 1° (bei m0=Pi/180).

2.)
Mikrokontroller für Taschenrechner: Können die nicht per Bit-Schieberei auch multiplizieren ?
-> einmal nach kinks geschoben = einmal mit 2 multipliziert, oder ist die Bitschieberei bloß ein Ergebnis von Addition mit sich selber?

So zum Abschluss noch Musik, diesmal zum entspannen (wenn's denn gefällt): et voila:

http://www.youtube.com/watch?v=KQ7b8PUEkuA

erstmal Gruß, Merman

(pssst, die Arbeit (hier am A.platz) bleibt schon wieder seit 2h liegen)

[richy]

Hi merman

Probiere mal die Simulation mit den exakten Konstanten aus und drucke den absoluten Fehler aus.
Setze
c1=cos(m0)
c2=sin(m0)
Als Extremtest mit wenigen Abtastwerten (z.B Pi/5) im Vergleich zu den Naeherungen. Die Naeherungen werden dann versagen und damit wird einiges deutlich. Ich hoffe du siehst, dass es unnoetig ist fuer C1 und C2 irgendwelche Naeherungen zu verwenden, ausser rein interessehalber. Aus Spass an der Freude :-) Oder wer weiss ...
Maple fuer Linux sollte in einer aelteren Version verfuegbar sein. Dann koennte man den Asci Quelltext direkt austauschen. MAPLE ist ideal fuer mathematisches Programmieren.
Dass unsere Verfahren gegenueber einer Taylorapproximation unabhaengig von einem Entwicklungszentrum ist liegt daran, dass wir eine Konstante verwenden. Und die Additionstheoreme sin(x+dx) cos(x+dx) gelten fuer alle x.

Stöhn, alleine die Vorarbeit:

Tja pures Ansi C kann sehr anstrengend sein :-)

(Mir fällt grad auf, ich hätte die Wurzelfunktion in der Schleife vermeiden können (wie besprochen), war aber auch so schon schnell)

Der Hauptvorteil der eleganten "Schraubenfedermethode" liegt darin, dass die Iteration dann nicht auf 0..180 Grad beschraenkt ist.

Ich vermute, dass ein Taschenrechner und andere Programme, sehr genäherte Startwerte verwenden (m0, c1, c2) um dann per Additionstheorem die Folgewerte zu berechnen.

Ich meine die Rechner verwenden heute noch den Cordic Algo. Der ist im Grunde aehnlich. Weitaus ausgefeilter und verwendet aber auch fest abgespeicherte Konstanten.

Allerdings gab es da noch die Anmerkung des Wiki-Mathematikers, dass das Halbieren (und Verdoppeln?) von Winkeln die Iterationsschritte nochmal verkürze.

Der Cordic Algo verwendet nur Multiplikationen mit 2. Das sind dann shifts, wie du sie bereits unter 2) beschrieben hast.
Der Mathematiker koennte noch etwas anderes gemeint haben :

Wollen wir den Sinus von 3.24 Grad berechnen, dann waere es unguenstig hier 324 Iterationen von 1/100 Grad durchzufuehren.
Effizienter sind
3 Iterationen von 1 Grad
2 Iterationen von 1/10 Grad
4 Iterationen von 1/100 Grad

Und dazu koenen wir die notwendigen Konstanten zuvor abspeichern :
c1[0]=cos(Pi/180)
c1[1]=cos(Pi/1800)
c1[3]=cos(Pi/18000) ebenso fuer C2

(Die Kostante c1 ist die Gleichsetzung von Strich mit Kreisbogenabschnitt, c1= 1-m0^2/2)

Strich=Gerade ?
Und eine Gerade ist nunmal kein Kreisbogen. Und das ist die (wohl einzigste) Naeherung in deiner graphischen Herleitung. Und zufaelligerweise entspricht dies einer Taylorreihe mit zwei Termen fuer cos(m0). Die Laenge des Kreisbogens waere exakt cos(m0). Vielleicht kannst du das noch herleiten. Das waere klasse, denn dann haettest du ein Additionstheoreme graphisch hergeleitet. Das waere unter Umstaenden tatsaechlich etwas fuer WIKI.

Meine c2 = wurzel(m0^2 - m0^4/4) ist nicht der Versuch einer Taylorreihe, der Term entstand aus der Herleitung c2=Wurzel(1-c1^2) (mit c1 = 1- m0^2/2)

Ja, das ist uns doch schon lange klar. Und c2=Wurzel(1-c1^2) ist sogar exakt. Aber weil dein c1 eine "Strichnaeherung" ist, ist c2 dann eben auch nur eine Naeherung. In deiner graphischen Herleitung muss c2=sin(m0) der exakte Wert sein. Kannst du mal eine etwas genauere Graphik deiner graphischen Herleitung hier reinstellen ?

Im Grunde weiss ich, was dich besonders herausfordert. Einen Sinus oder Cosinus praktisch aus der Luft zu zaubern. Ich meine zwar, dass das wohl "irgendwie kaum" moeglich ist, aber finde es dennoch interessant.

D.h. die Verhulst Gleichung fuer r=4 zeigt, dass es vielleicht doch moeglich ist.
Siehe (*) im Beitrag

Ich hoffe du hast inzwischen erkannt, dass alleine die Konstanten C1 und C2 entscheidend sind. Fuer C1 hast du (ohne es zu wissen) Taylor verwendet. Fuer C2 ebenfalls eine Naeherung. Wurzel(1-C1_Taylor^2). Meine letzten Fehlergrafiken zeigen, dass diese Naeherungen fuer m0 gegen 0 natuerlich gegen die exakten Werte konvergieren :
sin(0)=0 und cos(0)=1
Was passiert nun, wenn wir ein ganz kleines m0 waehlen und dieses in jedem Iterationsschritt vergroessern ? Indem wir fuer cos(m0) und sin(m0) die berechneten sin/cos Werte verwenden.

Das ist unsere elegante Schleife

> for n from 1 to M do
> x[n+1]:=x[n]*c1 - y[n]*c2; # -> Cosinuswerte
> y[n+1]:=y[n]*c1 + x[n]*c2; # -> Sinuswerte
> od:


Und jetzt bestmmen wir daraus unsere neuen Konstanten

> for n from 1 to M do
> x[n+1]:=x[n]*c1 - y[n]*c2; # -> Cosinuswerte
> y[n+1]:=y[n]*c1 + x[n]*c2; # -> Sinuswerte
> c1:=x[n+1];
> c2:=y[n+1];
> od:

(*)
Was wird passieren ? Unser m0 wir exponentiell anwachsen.
Genau so verhaelt sich auch die Loesung der Verhulst Gleichung fuer r=4 :



So schliesst sich mancher Kreis zwischen einer Merman Approximation und der Verhulst Gleichung wie man es anfangs vieleicht gar nicht vermutet. Nicht :-)
Die Verhulst Gleichung fuer r=4 produziert in etwa das was du suchst.

x(n+1)=4*x(n)*(1-x(n))
x(0)=x0

Du darfst sie dazu aber nicht ueber die Iterationsschritte betrachten, das ist eine chaotische Funktion, sondern ueber alle Anfangswerte x0 fuer einen Iterationsschritt. Und das sieht dann in der zentrierten Verhulst DZG wie folgt aus :



Und das ist ein (frequenzmodulierte) Kosinusfunktion, ohne dass wir irgendeine Information ueber einen Sinus oder Kosinus in dieser Gleichung verwendet haben. Und dass dies ein Kosinus ist, hoert man auch an diesem mp3 File. der die Verhulstgleichung fuer r=4 als Basedrum verwendet :

http://home.arcor.de/richardon/2011/chic0.mp3

Aus Verhulst und Kunst
http://www.quanten.de/forum/showthread.php5?t=2078


Ok dein Vorhaben ist trotz aller standartmathematischen Vorbehalte "irgendwie" realisierbar. Das Problem ist. Diese Vehulst Loesung, der Cosinus ist exponentiell frequenzmoduliert.
Deine Approximation koennte ein Ansatz sein, ein Gedankenanstoss um hier vieleicht weiter zu kommen. Schonmmal danke dafuer.

Viele Gruesse

[richy]

Deine Links

http://www.youtube.com/watch?v=Ddn4MGaS3N4
Hey das ist klasse. Super !

Dein afrikanisches Video :
http://www.youtube.com/watch?v=KQ7b8PUEkuA
Naja letzendlich nahm unsere ganze Kultur, wenigstens hier in Europa wohl von Afrika aus ihren Weg.

Angelique Kidjo hab von Anfang an mitverfolgt auch schon in den 90 ern mal live gesehen. Die absolute Powerfrau. Naja jetzt ist sie auch schon bischen aelter. Fuer mich eine der aussergewoehnlichsten afrikanischen Saengerinen. Geniale Frau :
http://www.youtube.com/watch?v=9IWBS...layer_embedded
Agolo oder Adouma war natuerlich bekannter.


Last not least Miss Grace Jones produced by Trevor Horn :
Typischer 80#s hi tecno Fairlight Synclavier african song :
Die Platte war damals aufgrund der Perfektion wie von einem andere Stern.
Das Video ist ein Tribute to Trevor Horn :
http://www.youtube.com/watch?v=crsb7fdWflU

[mermanview]

Ich hoffe du hast inzwischen erkannt, dass alleine die Konstanten C1 und C2 entscheidend sind.

... ähämm; die Abhängigkeit der Genauigkeit habe ich bereits vor einem Jahr bei Wiki erwähnt.
Ich bewege mich vielleicht in den Talsohlen der Mathematik, dennoch kann ich auch da zwingendene Logik erkennen.

Mathematische Näherung des ersten Sinuswertes:

r =Pi/180) (entspricht einem Grad, läßt sich für genauere Ergebnisse beliebieg verkleinern)

By the way:

bei

m0=1/10^p

legt p die Nachkommastellen zur Bestimmung von Pi/2 fest.

Nicht Zitat, sondern Hervorhebung:

n * m0 = Pi/2 mit p Nachkommastellen Genauigkeit, wenn x(n) * x1 - y(n) *y1 =0 (oder <= m0)

(da 90° = Pi/2 und cos(90)=0)

Wähle ich p=20, dann ergibt die Iteration bis x(n)*x1-y(n)*y1 = 0 -> Pi/2 mit einer Genauigkeit von 20 Nachkommastellen.
Ich kanns nicht beschwören, aber MAPLE müsste zeigen, dass auch die Cosinis/Sinus Werte ähnlich genau sind.

Kein Zitat:

Hervorhebung

WOMIT DENN AUCH DER LETZTE SCHRITT GETAN WÄRE; JUHUU:

ICH KANN OHNE KENNTNISS DER KREISZAHL PI, DIE KREISZAHL PI MIT HOHER GENAUIGKEIT BESTIMMEN,
SO KANN ICH AUF GLEICHEM WEG MIT GLEICHER GENAUIGKEIT DIE LÄNGE DES KREISBOGENABSCHNITTES FÜR 1° BESTIMMEN (= c1).

:- ) :- ) :- ) :- ) :- ) :- ):- ) :- ) :- ):- ) :- ) :- ) :- ) :- ) :- ) :- ) :- ) :- ) :- ) :- ) :- ) :- ) :- ) :- ) :- )

Damit ist die ursprüngliche Näherung reichlich genähert, der Strich/ die Gerade für 1° wird zur feinen eckigen Kurve.
Die Methode "Näherung plus Additionstheorem" verfeinert sich selber, zwecks Bestimmung der Anfangskonstanten.

Kannst du mal eine etwas genauere Graphik deiner graphischen Herleitung hier reinstellen ?

'Tschulidgung, hätte ich schon längst tun sollen, mal sehn ob ich es sofort jetzt hinbekomme.
(hängt davon ab wie lang die Kleinen noch schlafen, bei lautem Geräusch alter Tastatur, Moment...)





Hab noch was für dich:
Meine erste, ursprüngliche Formel zur Herleitung der Sinuswerte.
Die ist ein Besweis dafür, wie anstelle von Fleiß auch Leidenschaft zu unmöglichen Ausmaßen einer Formel führen kann.
Die Formel ergibt die gleichen Werte wie die Merman- Iteration, allerdings kann man sie eher als Tapetenmuster oder Stilleben verwenden.

So da ist sie:

(nach dem diese Formel stand (drei Nächte Umformung, ca. 50.000 mal vertan), hatte ich keine Lust mehr rauszukürzen,
...bin umgeschwenkt auf Achsenschwenk und Vektorkonstruktion)




cu

Merman

[mermanview]

Hallo richy,

ich habs geahnt:

Winkel - Halbierung ist der eigentliche Knaller bei der Bestimmung von Sinuswerten und co..

Wie ich letztens erwähnte:

Allerdings gab es da noch die Anmerkung des Wiki-Mathematikers, dass das Halbieren (und Verdoppeln?) von Winkeln die Iterationsschritte nochnal verkürze.
Ich vermute auch dahinter steckt eine die mathematische Umsetzung einer Geometrischen Logik, die in unserer Sinusfunktion noch nicht enthalten ist.

... bin der Sache mit meiner Methode auf den Grund gegangen (Koordinatensystem, logische Geometrie, + bißchen Mathe..)

Man erhält mit der Methode zumindest genaue Anfangswerte.

Nehmen wir einen Kreis und unterteilen ihn in 360 / 400 / oder 2 *Pi Winkelgrade, egal:

Halbieren, und nochmals halbieren führt stets zu bekannten Teilwerten der Gesamtzahl. Zum zweiten kann man Koordinaten, Steigungen (Tangens) usw. beim Halbieren leicht berechnen, so dass man zu Winkelgraden auch noch Höhen (sin) und Längen (cos) herleiten kann:


Bei jeder Iterationen führt immer die vorhergehende Steigung m zwischen Nullpunkt und den x/y Koordinaten zur den Folge-Koordinaten (x(n+1)/y(n+1), diese ergeben dann wieder die Folgesteigung m(n+1).

m(n) = (1-x(n)) / y(n)

x(n+1) = Wurzel(1 / (m(n)^2+1))

y(n+1) = m(n) * x(n+1)

m(n+1)= (1-x(n+1) / y(n+1)

Bei nur 8 Iterationen erhält man den genauen Anfangswert für 90°/2^8 Grad (90°/256 = 360°/1024)
Aus der früheren Näherungs-Geraden wurde ein runder Kreisbogen !!!

by the way: Im digitalen Zeitalter sollte man den Kreis eh in 1024 Teile zerlegen.

Gruß Merman